Leetcode 第三周周赛总结(第 50 场双周赛)
本文共 2760 字,大约阅读时间需要 9 分钟。
文章目录
排名及做题情况(做了三道题 第四道题实在连下手都下不去 放弃了)


闲聊
其实我一直在想 现在我觉得打周赛真的有那么有意义吗
其实吧 我觉得还是挺有意义的 感觉就跟高考是一个道理嘛 到时候面试的时候也是限时给出几道题虽然说 面试算法题肯定也不是全部 但是也是很重要一部分
像这种限时题 做起来的感觉就是跟面试面题一样 刚开始你想的方法都是你本能想要拿出来的方法 模拟那种感觉吧第一题 5717. 最少操作使数组递增 Easy
原题题目
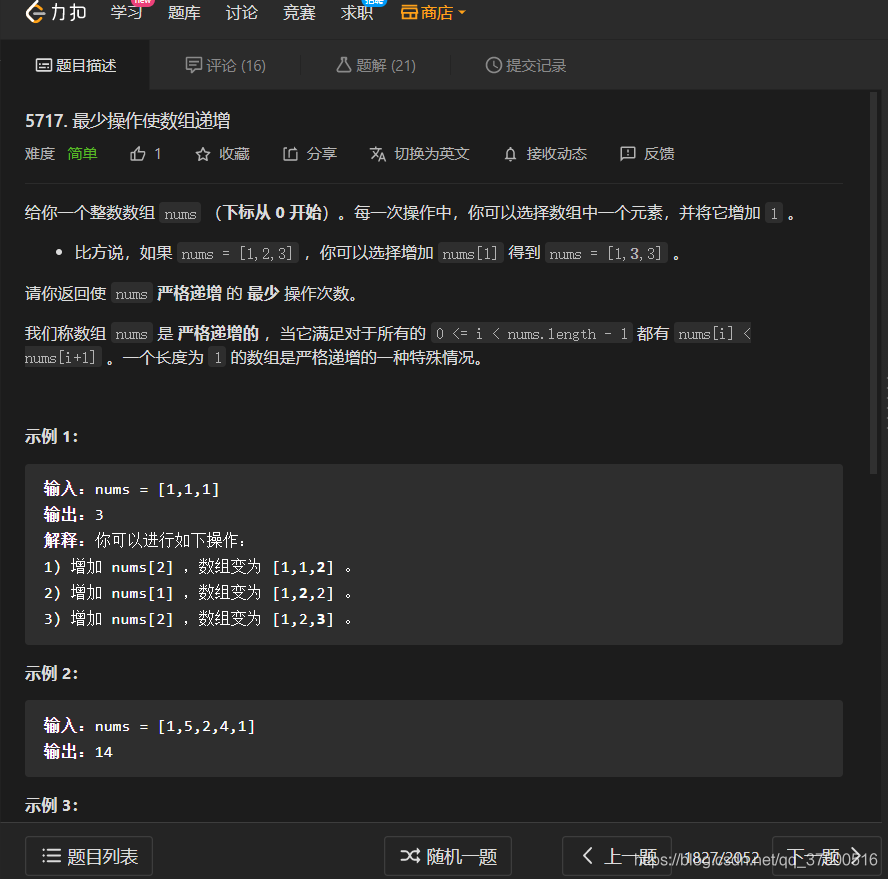
第一题 比赛AC代码
class Solution { public: int minOperations(vector & nums) { int ret = 0; for(int i=1;i 第二题 5718. 统计一个圆中点的数目 Med
原题题目
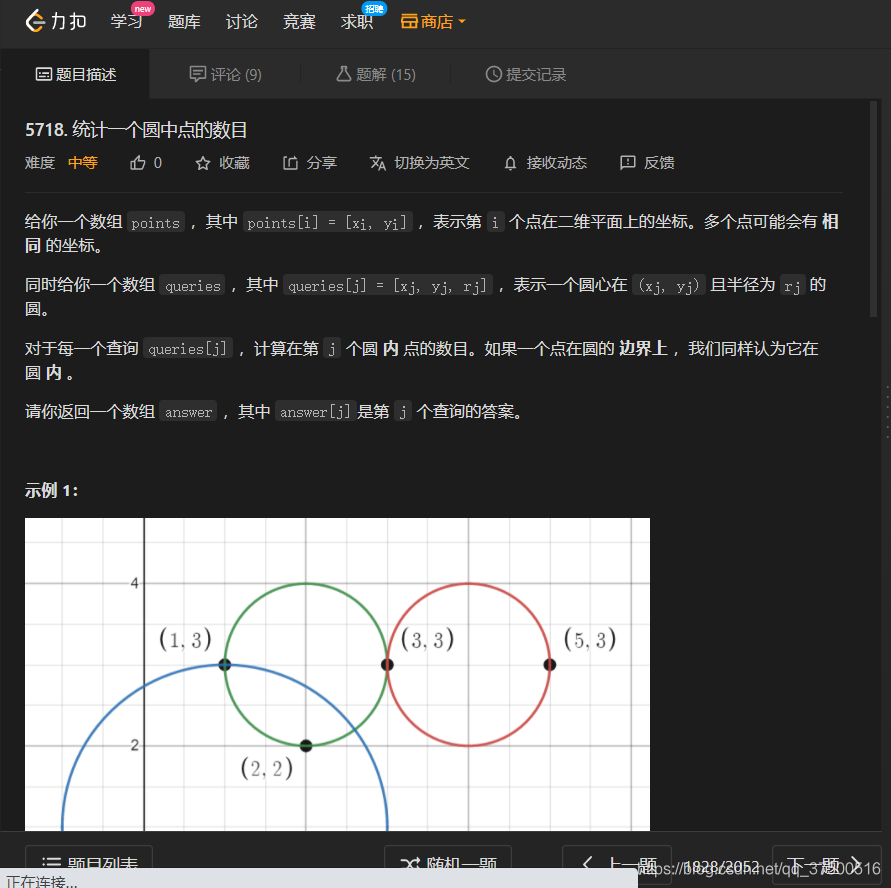
第二题 比赛AC代码
class Solution { public: vector countPoints(vector >& points, vector >& queries) { int size = queries.size(); vector ret(size,0); for(const auto& point:points) { int x = point[0],y = point[1]; for(int i=0;i = queries[i][0] - r && x <= queries[i][0] + r && y >= queries[i][1] - r && y<= queries[i][1] + r) if(pow(abs(queries[i][0] - x),2) + pow(abs(queries[i][1] - y),2) <= pow(r,2)) ++ret[i]; } } return ret; }}; 第三题 5719. 每个查询的最大异或值 Med
原题题目
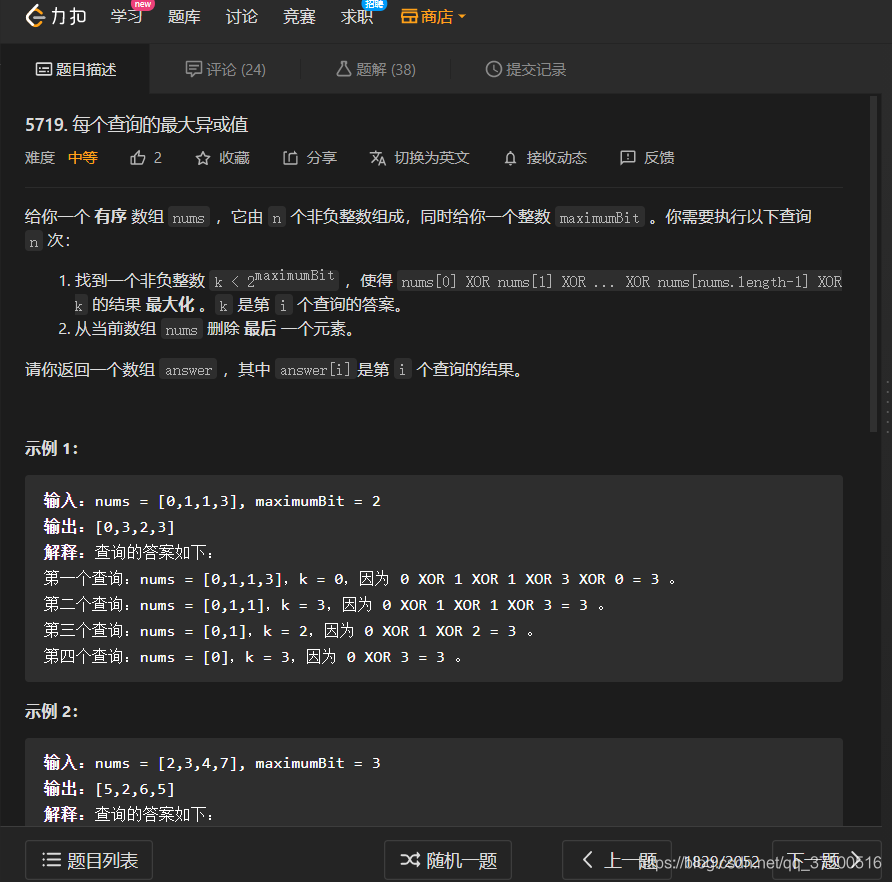
第三题 比赛AC代码
class Solution { public: vector getMaximumXor(vector & nums, int maximumBit) { int size = nums.size(); vector ret(size,INT_MIN); int judge = (1< 第四题 裂开题 直接跳过 CV人家代码 Hard
原题题目
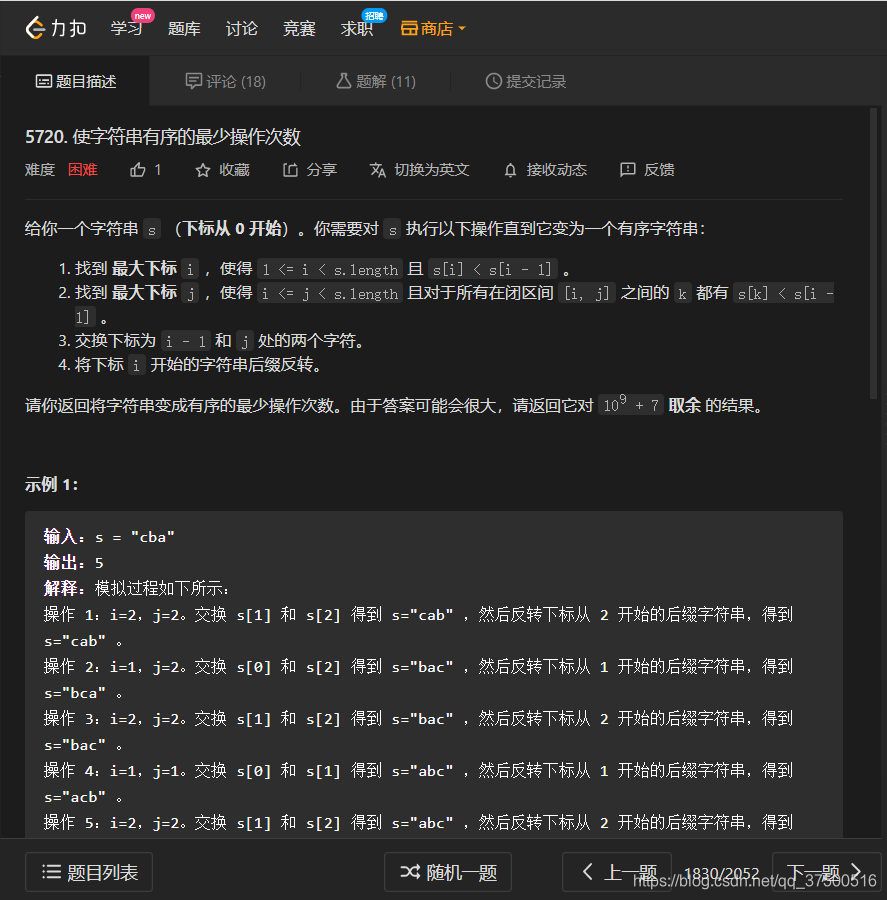
第四题 裂开题 CV官方代码
class Solution { private: static constexpr int mod = 1000000007; using LL = long long; public: // 快速幂,用来计算 x^y mod m int quickmul(int x, int y) { int ret = 1, mul = x; while (y) { if (y & 1) { ret = (LL)ret * mul % mod; } mul = (LL)mul * mul % mod; y >>= 1; } return ret; } int makeStringSorted(string s) { int n = s.size(); // fac[i] 表示 i! mod m // facinv[i] 表示 i! 在 mod m 意义下的乘法逆元 vector fac(n + 1), facinv(n + 1); fac[0] = facinv[0] = 1; for (int i = 1; i < n; ++i) { fac[i] = (LL)fac[i - 1] * i % mod; // 使用费马小定理 + 快速幂计算乘法逆元 facinv[i] = quickmul(fac[i], mod - 2); } // freq 存储每个字符出现的次数 vector freq(26); for (char ch: s) { ++freq[ch - 'a']; } int ans = 0; for (int i = 0; i < n - 1; ++i) { // rank 求出比 s[i] 小的字符数量 int rank = 0; for (int j = 0; j < s[i] - 'a'; ++j) { rank += freq[j]; } // 排列个数的分子 int cur = (LL)rank * fac[n - i - 1] % mod; // 依次乘分母每一项阶乘的乘法逆元 for (int j = 0; j < 26; ++j) { cur = (LL)cur * facinv[freq[j]] % mod; } ans = (ans + cur) % mod; --freq[s[i] - 'a']; } return ans; }}; 转载地址:http://ncni.baihongyu.com/
你可能感兴趣的文章